14. Chapter 2 & 9: Two-Way Tables#
When analyzing relationships between two variables, it’s important to determine whether the variables are quantitative or categorical:
Two Quantitative variables are analyzed using scatterplots, examining the relationship, and fitting a line to the data if it is approximately linear.
One Quantitative and one Categorical: We can describe the distribution of the quantitative variable for each value of the categorical variable.
Two Categorical variables are analyzed using counts (frequencies) or percents (relative frequencies). We can use a two-way table to summarize the raw data that gives counts of observations for each combination of values of the two categorical variables.
14.1. The two-way table#
A two-way table displays counts of observations for each combination of values of two categorical variables.
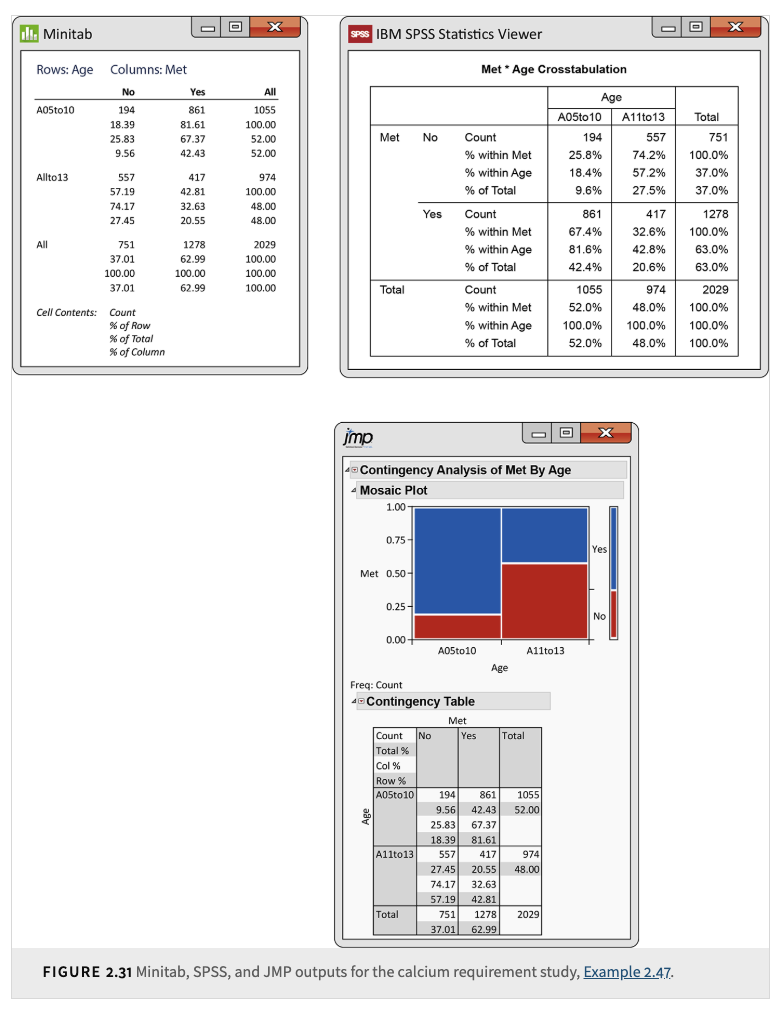
Example 2.40: Is the calcium intake adequate?
The table summarizes whether children met the calcium requirement based on their age group (5 to 10 years or 11 to 13 years):
There are 2,029 children in the study.
Each child’s calcium intake is classified as meeting or not meeting the requirement.
Met Requirement |
5 to 10 |
11 to 13 |
|---|---|---|
No |
194 |
557 |
Yes |
861 |
417 |
The row variable is “Met Requirement,” and the column variable is “Age Group.”
Adding margins helps to summarize the data by showing totals for each row and column.
Example 2.41: Add the margins to the table
Met Requirement |
5 to 10 |
11 to 13 |
Total |
|---|---|---|---|
No |
194 |
557 |
751 |
Yes |
861 |
417 |
1278 |
Total |
1055 |
974 |
2029 |
There were 1,055 children aged 5 to 10 and 974 children aged 11 to 13.
The total number of children who did not meet the calcium requirement is 751.
The row variable indicates whether the requirement was met.
The column variable indicates the age group.
Each cell in the table corresponds to a specific combination of row and column variables.
The joint distribution shows the proportion of each cell in relation to the total sample size.
Example 2.42: The Joint Distribution
Met Requirement |
5 to 10 |
11 to 13 |
|---|---|---|
No |
0.0956 |
0.2745 |
Yes |
0.4243 |
0.2055 |
The sum of the joint distribution proportions is approximately 1 (\(\approx 0.9999\) due to rounding).
This table helps determine targeted interventions based on age groups and calcium intake.
A marginal distribution provides the distribution of one categorical variable in a two-way table.
Example 2.43: Marginal Distribution of Age
Age Group |
Proportion |
|---|---|
5 to 10 |
0.52 |
11 to 13 |
0.48 |
In this sample, 52% of the children are aged 5 to 10, and 48% are aged 11 to 13.
Example 2.44: Marginal Distribution of Met Requirement
This table shows the distribution of whether children met the calcium requirement:
Met Requirement |
Percent |
|---|---|
No |
37.01% |
Yes |
62.99% |
The majority of children (about 63%) meet the recommended calcium intake.
Graphical Representation:
Marginal distributions can be visualized using bar graphs or pie charts. These displays are useful when summarizing more complex tables. For this example:
52% of children are aged 5 to 10.
37% of children do not meet the calcium requirement.
Graphical displays provide an immediate summary of the data, especially when multiple rows or columns are involved.
In Example 2.45, we examined the conditional distribution of Met Requirement for children aged 5 to 10. This is an example of conditioning on the value of age to calculate the distribution of Met Requirement.
Example 2.46: Conditional Distribution of Met Requirement for Children Aged 5 to 10
Met Requirement |
No |
Yes |
|---|---|---|
Percent |
18.39% |
81.61% |
These percentages sum to 100%. In this group, 81.61% met the requirement, while 18.39% did not.
Bar Graphs and Interpretation
Bar graphs are helpful in visualizing relationships between two categorical variables. They do not provide a single numerical summary (like correlation) but allow for flexible comparisons based on chosen categories.
Warning
A two-way table contains a great deal of information in a compact form. Accurately interpreting this information often requires calculating appropriate percentages. It is advisable to use software for computations to ensure accuracy when interpreting joint, marginal, and conditional distributions.
14.2. Simpson’s paradox and two-way tables#
Simpson’s paradox happens when the pattern (or relationship) you observe in one two-way table reverses or disappears once you combine data across additional categories—often introducing a third variable (making it effectively a three-dimensional table).
Simpson’s paradox is a reminder to look out for hidden or confounding variables and to be careful with aggregate data.
It encourages further investigation into subgroup-level patterns before drawing conclusions.
A Concrete Example:
Separate Subgroup Tables:
Imagine we have a medical trial with two subgroups based on disease severity: Mild and Severe.
Subgroup 1 (Mild Cases)
Improved
Not Improved
Row Total
Treatment
80
20
100
Control
45
15
60
Column Totals
125
35
160
Treatment success rate = \(80/100 = 80\%\)
Control success rate = \(45/60 = 75\%\)
Subgroup 2 (Severe Cases)
Improved
Not Improved
Row Total
Treatment
20
80
100
Control
9
41
50
Column Totals
29
121
150
Treatment success rate = \(20/100 = 20\%\)
Control success rate = \(9/50 = 18\%\)
Observation: In both subgroups (Mild and Severe), the Treatment group outperforms the Control group (80% > 75% in Mild; 20% > 18% in Severe).
Combined Two-Way Table:
Now suppose you combine the data (ignoring disease severity):
Improved
Not Improved
Row Total
Treatment
100
100
200
Control
54
56
110
Column Totals
154
156
310
Treatment success rate (overall) = \(100/200 = 50\%\)
Control success rate (overall) = \(54/110 \approx 49.1\%\)
Key Point: Here, we only see a small overall difference (50% vs. 49.1%). But with different numbers or proportions of Mild vs. Severe cases, the overall results could flip. For instance, we might see Control appear better than Treatment once the data is combined — that flip is Simpson’s paradox in action.
Simpson’s paradox shows that conclusions drawn from aggregated data may differ from those drawn from the analysis of disaggregated data. Always consider the possibility of lurking variables when interpreting statistical results.
Additional Example Intuition:
Imagine two hospitals, A and B, where the success rate of a certain surgery appears higher for Hospital A when considering all surgeries together. However, if we separate the surgeries based on whether they were for high-risk or low-risk patients:
Hospital B might have better success rates for both high-risk and low-risk surgeries.
Hospital A may have treated a disproportionately higher number of low-risk patients (easier surgeries), inflating its overall success rate.
Thus, the aggregation ignores the differences in patient risk, leading to a misleading conclusion.
Summary: Simpson’s paradox reveals how misleading it can be to interpret aggregated data without considering the influence of lurking variables. It demonstrates the importance of:
Breaking down the data by relevant subgroups.
Accounting for confounding factors in the analysis.
Interpreting results carefully, especially when making decisions based on combined statistics.
Warning
Always check for lurking variables or potential confounding factors when interpreting aggregated data. Simpson’s paradox serves as a reminder that aggregated statistics can be misleading without careful analysis of underlying subgroups.
14.3. Inference of two-way tables#
Below is an overview of the key ideas, steps, and basic mathematical derivations for inference on two-way (contingency, crosstab) tables in statistics. We’ll focus on the classical approaches: Chi-square tests,
Below is a contingency table showing gender (Male, Female) by product preference (Product A, Product B).
Product A |
Product B |
Total |
|
|---|---|---|---|
Male |
40 |
20 |
60 |
Female |
50 |
30 |
80 |
Total |
90 |
50 |
140 |
Here:
Rows represent gender (Male and Female).
Columns represent product preference (Product A and Product B).
Each cell contains the count of observations for that combination.
Chi-Square Test of Independence: The Chi-Square Test of Independence is used with contingency tables to determine if there is a significant association between two categorical variables.
Null Hypothesis \(H_0\): The two variables are independent.
Alternative Hypothesis \(H_a\): The two variables are not independent.
The expected count for each cell is calculated under the assumption that the two variables are independent. The formula is:
Using the gender vs. product table:
Row Totals: Male = 60, Female = 80
Column Totals: Product A = 90, Product B = 50
Grand Total = 140
Example: Expected count for (Male, Product A):
Similarly:
\(E_{\text{Male, B}} = \frac{(60 \times 50)}{140} = 21.43\)
\(E_{\text{Female, A}} = \frac{(80 \times 90)}{140} = 51.43\)
\(E_{\text{Female, B}} = \frac{(80 \times 50)}{140} = 28.57\)
Summary Table: Observed vs. Expected: Below we combine observed (\(O\)) and expected (\(E\)) counts:
Product A (O) |
Product A (E) |
Product B (O) |
Product B (E) |
|
|---|---|---|---|---|
Male |
40 |
38.57 |
20 |
21.43 |
Female |
50 |
51.43 |
30 |
28.57 |
The Chi-Square statistic is:
where
\(O\) is the observed count
\(E\) is the expected count
We compute \(\frac{(O - E)^2}{E}\) for each cell and sum them up:
(Male, Product A): \(\frac{(40 - 38.57)^2}{38.57} \approx 0.053\)
(Male, Product B): \(\frac{(20 - 21.43)^2}{21.43} \approx 0.095\)
(Female, Product A): \(\frac{(50 - 51.43)^2}{51.43} \approx 0.040\)
(Female, Product B): \(\frac{(30 - 28.57)^2}{28.57} \approx 0.072\)
Summing:
Degrees of Freedom: For a Chi-Square test of independence:
where \(r\) = number of rows, \(c\) = number of columns.
In this 2×2 example:
Interpreting the Results: To interpret the result, compare the calculated \(\chi^2\) to a critical value from the Chi-Square distribution with 1 degree of freedom at \(\alpha = 0.05\).
Critical value at df = 1, \(\alpha = 0.05\): 3.84.
Our \(\chi^2 = 0.26\) is much less than 3.84.
Hence, do not reject \(H_0\). The data does not suggest a significant association between gender and product preference here.
For larger than 2×2 tables:
All cells should have expected counts of at least 1.
Fewer than 20% of cells have expected counts under 5.
For a 2×2 table (smallest case):
All cells must have expected counts of at least 5.
If these conditions fail, consider Fisher’s Exact Test.
Formula:
Why? Under independence:
\(P(A_i) = \frac{\text{Row total for }A_i}{n}\)
\(P(B_j) = \frac{\text{Column total for }B_j}{n}\)
Then,
so the expected count in cell \((i,j)\) is
Standardized Residual: The standardized residual measures how far \(O\) is from \(E\), relative to the standard deviation:
Small \(|Z|\) means \(O \approx E\).
Large \(|Z|\) indicates a big deviation from expectation.
For large samples, \(Z\) often approximates a standard normal distribution \(N(0,1)\) under the null hypothesis.
We can also view the Chi-Square statistic as summing the squares of these standardized residuals:
If \(\chi^2\) is close to zero, \(O_{ij} \approx E_{ij}\) in all cells, supporting independence.
If \(\chi^2\) is large, it suggests a significant departure from \(H_0\) and evidence of an association.
Important
Before using the Chi-Square test, ensure expected counts are large enough (≥ 5 for 2×2). Otherwise, use Fisher’s Exact Test.
Warning
The Chi-Square test assumes a sufficiently large sample size. If you have too many low expected counts, results may be unreliable.
